Matryoshka Embeddings: Detail at Multiple Scales
What are Matryoshka Embeddings?
When building efficient vector search systems, one key challenge is managing storage costs while maintaining acceptable latency and recall. Modern embedding models output vectors with hundreds or thousands of dimensions, creating significant storage and computational overhead for the raw vector and index.
Traditionally, the storage requirements are reduced by applying a quantization or dimensionality reduction method just before building the index. For instance, we can save storage by lowering the precision using Product Quantization (PQ) or the number of dimensions using Principal Component Analysis (PCA). These methods analyze the entire vector set to find a more compact one that maintains the semantic relationships between vectors.
While effective, these standard approaches reduce precision or dimensionality only once and at a single scale. But what if we could maintain multiple layers of detail simultaneously, like a pyramid of increasingly precise representations?
Enter Matryoshka embeddings. Named after Russian nesting dolls (see illustration), these clever constructs embed multiple scales of representation within a single vector. Unlike traditional post-processing methods, Matryoshka embeddings learn this multi-scale structure during the initial training process. The result is remarkable: not only does the full embedding capture input semantics, but each nested subset prefix (first half, first quarter, etc.) provides a coherent, if less detailed, representation.
 Figure: Visualization of Matryoshka embeddings with multiple layers of detail
Figure: Visualization of Matryoshka embeddings with multiple layers of detail
Figure: Visualization of Matryoshka embeddings with multiple layers of detail
This approach contrasts sharply with conventional embeddings, where using arbitrary subsets of the vector dimensions typically destroys semantic meaning. With Matryoshka embeddings, you can choose the granularity that best balances your specific task’s precision and computational cost.
Need a quick approximate search? Use the smallest “doll.” Need maximum accuracy? Use the full embedding. This flexibility makes them particularly valuable for systems adapting to different performance requirements or resource constraints.
Inference
A valuable application of Matryoshka embeddings is accelerating similarity searches without sacrificing recall. By leveraging smaller subsets of query and database embeddings—such as the first 1/32 of their dimensions—we can build an index over this reduced space that still preserves much of the similarity information. Initial results from this smaller embedding space can be used directly. Still, there’s also a technique to boost recall and account for any minor reduction from the dimensional cutback, making this approach both efficient and effective for similarity search tasks.
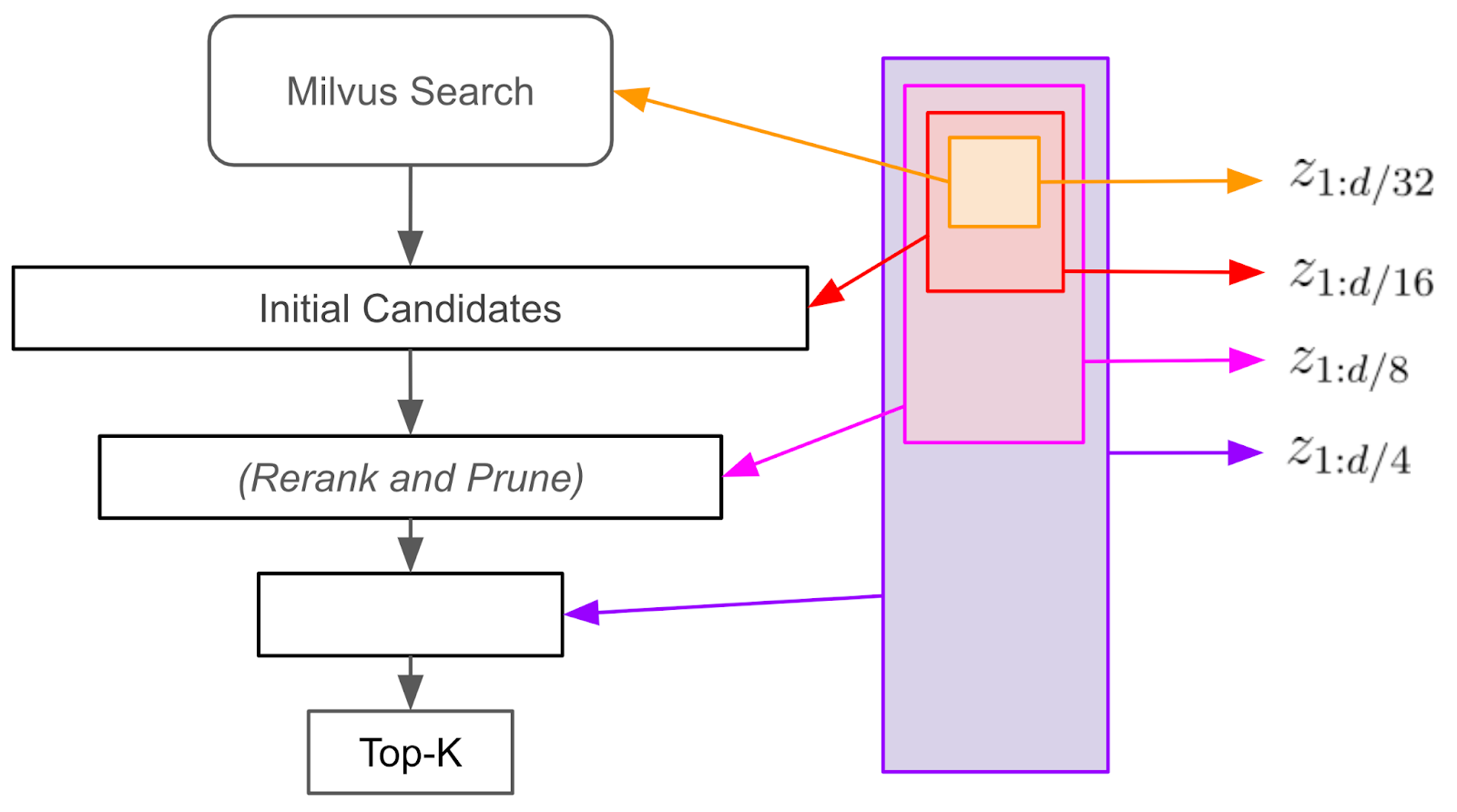 Figure: How the funnel search works with Matryoshka embeddings
Figure: How the funnel search works with Matryoshka embeddings
Figure: How the funnel search works with Matryoshka embeddings
To efficiently speed up similarity search while maintaining accuracy, we can use a “funnel search” approach. First, we perform an initial similarity search using only the first 1/32 of the embedding dimensions, generating a broad pool of candidate items. We then rerank these candidates based on their similarity to the query using the first 1/16 of the dimensions, pruning a portion of the list. This process continues iteratively, reranking and pruning with increasingly larger subsets of the embedding dimensions—1/8, 1/4, and so on. Importantly, we only perform one initial similarity search in this lower-dimensional space, and a single pass of the embedding model computes the query embedding. This funneling process narrows down candidates at each step and is faster and more efficient than directly searching in the full-dimensional space. Drawing many matches from the 1/32-dimensional space and refining them through funnel search can significantly accelerate similarity search while preserving strong recall.
Training
Let’s go into a few of the technical details. The method is very simple to apply. Consider the context of fine-tuning a BERT model for sentence embedding. To convert a BERT model, which has been pre-trained on the masked-token loss, into a sentence embedding model, we form the sentence embedding as the average of the final layer, that is, the average of the per-token contextualized embeddings.
One choice of training objective is the Cosine Sentence (CoSENT) loss, . It inputs a pair of sentence embeddings, , and their desired similarity score, (see the link above for the formula). Now, to learn Matryoshka embeddings, we make a small modification to the training objective:
where the sum is continued by calculating the loss on half of the input to the previous term until an information bottleneck is reached. The authors suggest setting
.
Simply put, the Matryoshka loss is a weighted sum of the original loss over recursive subsets of the input.
One key takeaway from the equation above is that the Matryoshka loss achieves efficient learning of representations at multiple scales by sharing weights across the embedding models (the same model is used to encode, for example, and ) and sharing dimensions across scales ( is a subset of ).
Matryoshka Embeddings and Milvus
Milvus seamlessly supports any Matryoshka embedding model that can be loaded via standard libraries such as pymilvus.model, sentence-transformers, or other similar tools. From the system’s perspective, there’s no functional difference between a regular embedding model and one specifically trained to generate Matryoshka embeddings.
Popular Matryoshka embedding models include:
OpenAI’s
text-embedding-3-largeNomic’s
nomic-embed-text-v1Alibaba’s
gte-multilingual-base
For a complete guide on using Matryoshka embeddings with Milvus, see the notebook Funnel Search with Matryoshka Embeddings.
Summary
Matryoshka embedding lets developers create shortened embeddings without sacrificing semantic integrity, making them ideal for more efficient search and storage. While you can modify an existing model, pre-trained options, such as those from OpenAI and Hugging Face, are also available.
However, a current limitation is the scarcity of open-source Matryoshka embeddings, with few available on the Hugging Face hub. Additionally, these models are often not explicitly labeled as “Matryoshka,” making them harder to locate. Hopefully, with growing interest, broader availability and clearer labeling may soon follow.
Ready to streamline your search capabilities? Get started with Milvus + Matryoshka embeddings today!
Resources
- What are Matryoshka Embeddings?
- Inference
- Training
- Matryoshka Embeddings and Milvus
- Summary
- Resources
On This Page
Try Managed Milvus for Free
Zilliz Cloud is hassle-free, powered by Milvus and 10x faster.
Get StartedLike the article? Spread the word