Gaussian DecayCompatible with Milvus 2.6.x

Gaussian decay, also known as normal decay, creates the most natural-feeling adjustment to your search results. Like human vision that gradually blurs with distance, Gaussian decay creates a smooth, bell-shaped curve that gently reduces relevance as items move away from your ideal point. This approach is ideal when you want a balanced decay that doesn’t harshly penalize items just outside your preferred range but still significantly reduces the relevance of distant items.

Unlike other decay rankers:

• Exponential decay drops sharply at first, creating a stronger initial penalty

• Linear decay decreases at a constant rate until reaching zero, creating a clear cutoff

Gaussian decay provides a more balanced, intuitive approach that feels natural to users.

When to use Gaussian decay

Gaussian decay is particularly effective for:

Use Case	Example	Why Gaussian Works Well
Location-based searches	Restaurant finders, store locators	Mimics natural human perception of distance relevance
Content recommendations	Article suggestions based on publication date	Gradual decline in relevance as content ages
Product listings	Items priced near a target	Smooth relevance decline as prices deviate from target
Expertise matching	Finding professionals with relevant experience	Balanced assessment of experience relevance

If your application requires a natural feeling of declining relevance without harsh penalties or strict cutoffs, Gaussian decay is likely your best choice.

Bell curve principle

Gaussian decay creates a smooth, bell-shaped curve that gradually reduces relevance as distance increases from an ideal point. Named after mathematician Carl Friedrich Gauss, this distribution appears frequently in nature and statistics, which explains why it feels so intuitive to human perception.

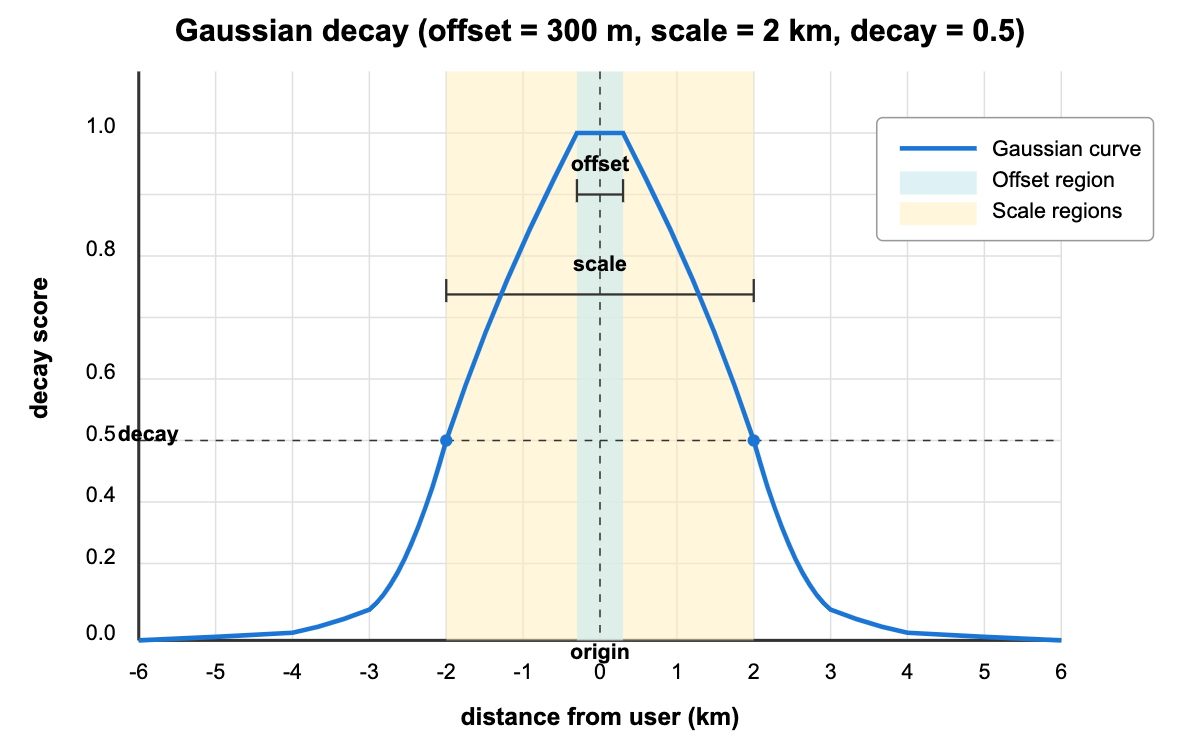Gaussian Decay

The graph above shows how Gaussian decay would affect restaurant rankings in a mobile search app:

• origin (0 km): Your current location, where relevance is at its maximum (1.0).

• offset (±300 m): The “perfect score zone” around you—all restaurants within 300 meters maintain full relevance scores (1.0), ensuring that very nearby options aren’t needlessly penalized for tiny distance differences.

• scale (±2 km): The distance at which relevance drops to the decay value—restaurants exactly 2 kilometers away have their relevance scores halved (0.5).

• decay (0.5): The score at the scale distance—this parameter essentially controls how quickly scores diminish with distance.

As you can see from the curve, restaurants beyond 2 km continue to decrease in relevance but never quite reach zero. Even restaurants 4-5 kilometers away retain some minimal relevance, allowing excellent but distant restaurants to still appear in your results (albeit ranked lower).

This behavior mimics how people naturally think about distance relevance—nearby places are preferred, but we’re willing to travel farther for exceptional options.

Formula

The mathematical formula for calculating a Gaussian decay score is:

$$S(doc) = \exp\left( -\frac{\left( \max\left(0, \left|fieldvalue_{doc} - origin\right| - offset \right) \right)^2}{2\sigma^2} \right)$$

Where:

$$\sigma^2 = -\frac{scale^2}{2 \cdot \ln(decay)}$$

Breaking this down in plain language:

1. Calculate how far the field value is from the origin: $|fieldvalue_{doc} - origin|$

2. Subtract the offset (if any) but never go below zero: $\max(0, distance - offset)$

3. Square this adjusted distance: $(adjusted\_distance)^2$

4. Divide by $2\sigma^2$, which is calculated from your scale and decay parameters

5. Take the negative exponent, which gives you a value between 0 and 1: $\exp(-value)$

The $\sigma^{2}$ calculation converts your scale and decay parameters into the standard deviation squared for the Gaussian distribution. This is what gives the function its characteristic bell shape.

Use Gaussian decay

Gaussian decay can be applied to both standard vector search and hybrid search operations in Milvus. Below are the key code snippets for implementing this feature.

Create a decay ranker

After your collection is set up with a numeric field (in this example, distance in meters from the user), create a Gaussian decay ranker:

from pymilvus import Function, FunctionType

# Create a Gaussian decay ranker for location-based restaurant search
ranker = Function(
    name="restaurant_distance_decay",     # Function identifier
    input_field_names=["distance"],       # Numeric field for distance in meters
    function_type=FunctionType.RERANK,    # Function type. Must be RERANK
    params={
        "reranker": "decay",              # Specify decay reranker
        "function": "gauss",              # Choose Gaussian decay
        "origin": 0,                      # Your current location (0 meters)
        "offset": 300,                    # 300m no-decay zone
        "decay": 0.5,                     # Half score at scale distance
        "scale": 2000                     # 2 km scale (2000 meters)
    }
)

Apply to standard vector search

After defining your decay ranker, you can apply it during search operations by passing it to the ranker parameter:

# Apply decay ranker to restaurant vector search
result = milvus_client.search(
    collection_name,
    data=["italian restaurants"],         # Query text
    anns_field="dense",                   # Vector field to search
    limit=10,                             # Number of results
    output_fields=["name", "cuisine", "distance"],  # Fields to return
    ranker=ranker,                        # Apply the decay ranker
    consistency_level="Strong"
)

Apply to hybrid search

Decay rankers can also be applied to hybrid search operations that combine multiple vector fields:

from pymilvus import AnnSearchRequest

# Define dense vector search request
dense = AnnSearchRequest(
    data=["italian restaurants"],
    anns_field="dense",
    param={},
    limit=10
)

# Define sparse vector search request
sparse = AnnSearchRequest(
    data=["italian restaurants"],
    anns_field="sparse_vector",
    param={},
    limit=10
)

# Apply decay ranker to restaurant hybrid search
hybrid_results = milvus_client.hybrid_search(
    collection_name,
    [dense, sparse],                      # Multiple search requests
    ranker=ranker,                        # Same decay ranker
    limit=10,
    output_fields=["name", "cuisine", "distance"]
)

For more information on hybrid search operations, refer to Multi-Vector Hybrid Search.