Similarity Metrics
In Milvus, similarity metrics are used to measure similarities among vectors. Choosing a good distance metric helps improve the classification and clustering performance significantly.
The following table shows how these widely used similarity metrics fit with various input data forms and Milvus indexes. Currently, Milvus supports various types of data, including floating point embeddings (often known as floating point vectors or dense vectors), binary embeddings (also known as binary vectors), and sparse embeddings (also known as sparse vectors).
| Metric Types | Index Types |
|---|---|
|
|
| Metric Types | Index Types |
|---|---|
|
|
| Metric Types | Index Types |
|---|---|
| IP |
|
Euclidean distance (L2)
Essentially, Euclidean distance measures the length of a segment that connects 2 points.
The formula for Euclidean distance is as follows:
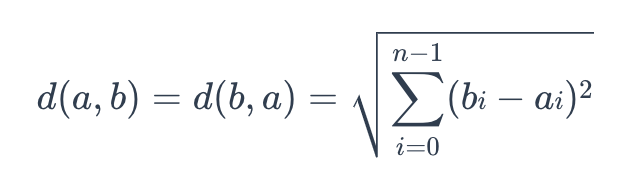 euclidean
euclidean
where a = (a0, a1,…, an-1) and b = (b0, b0,…, bn-1) are two points in n-dimensional Euclidean space
It’s the most commonly used distance metric and is very useful when the data are continuous.
Inner product (IP)
The IP distance between two vector embeddings are defined as follows:
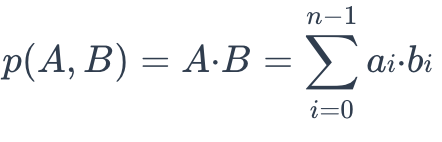 ip
ip
IP is more useful if you need to compare non-normalized data or when you care about magnitude and angle.
If you apply the IP distance metric to normalized embeddings, the result will be equivalent to calculating the cosine similarity between the embeddings.
Suppose X’ is normalized from embedding X:
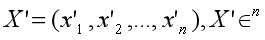 normalize
normalize
The correlation between the two embeddings is as follows:
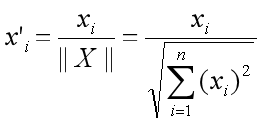 normalization
normalization
Cosine Similarity
Cosine similarity uses the cosine of the angle between two sets of vectors to measure how similar they are. You can think of the two sets of vectors as two line segments that start from the same origin ([0,0,…]) but point in different directions.
To calculate the cosine similarity between two sets of vectors A = (a0, a1,…, an-1) and B = (b0, b1,…, bn-1), use the following formula:
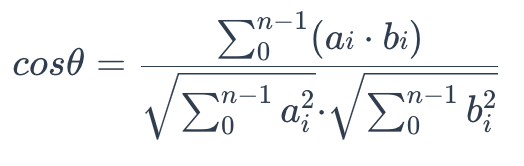 cosine_similarity
cosine_similarity
The cosine similarity is always in the interval [-1, 1]. For example, two proportional vectors have a cosine similarity of 1, two orthogonal vectors have a similarity of 0, and two opposite vectors have a similarity of -1. The larger the cosine, the smaller the angle between two vectors, indicating that these two vectors are more similar to each other.
By subtracting their cosine similarity from 1, you can get the cosine distance between two vectors.
Jaccard distance
Jaccard similarity coefficient measures the similarity between two sample sets and is defined as the cardinality of the intersection of the defined sets divided by the cardinality of the union of them. It can only be applied to finite sample sets.
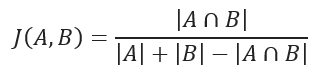 Jaccard similarity coefficient
Jaccard similarity coefficient
Jaccard distance measures the dissimilarity between data sets and is obtained by subtracting the Jaccard similarity coefficient from 1. For binary variables, Jaccard distance is equivalent to the Tanimoto coefficient.
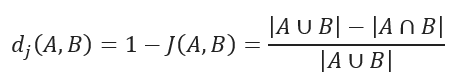 Jaccard distance
Jaccard distance
Hamming distance
Hamming distance measures binary data strings. The distance between two strings of equal length is the number of bit positions at which the bits are different.
For example, suppose there are two strings, 1101 1001 and 1001 1101.
11011001 ⊕ 10011101 = 01000100. Since, this contains two 1s, the Hamming distance, d (11011001, 10011101) = 2.
Structural Similarity
When a chemical structure occurs as a part of a larger chemical structure, the former is called a substructure and the latter is called a superstructure. For example, ethanol is a substructure of acetic acid, and acetic acid is a superstructure of ethanol.
Structural similarity is used to determine whether two chemical formulae are similar to each other in that one is the superstructure or substructure of the other.
To determine whether A is a superstructure of B, use the following formula:
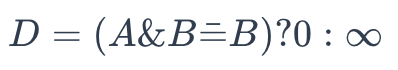 superstructure
superstructure
Where:
- A is the binary representation of a chemical formula to be retrieved
- B is the binary representation of a chemical formula in the database
Once it returns 0, A is not a superstructure of B. Otherwise, the result is the other way around.
To determine whether A is a substructure of B, use the following formula:
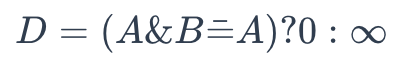 substructure
substructure
Where:
- A is the binary representation of a chemical formula to be retrieved
- B is the binary representation of a chemical formula in the database
Once it returns 0, A is not a substructure of B. Otherwise, the result is the other way around.
FAQ
Why is the top1 result of a vector search not the search vector itself, if the metric type is inner product?
This occurs if you have not normalized the vectors when using inner product as the distance metric.
What is normalization? Why is normalization needed?
Normalization refers to the process of converting an embedding (vector) so that its norm equals 1. If you use Inner Product to calculate embeddings similarities, you must normalize your embeddings. After normalization, inner product equals cosine similarity.
See Wikipedia for more information.
Why do I get different results using Euclidean distance (L2) and inner product (IP) as the distance metric?
Check if the vectors are normalized. If not, you need to normalize the vectors first. Theoretically speaking, similarities worked out by L2 are different from similarities worked out by IP, if the vectors are not normalized.What’s next
- Learn more about the supported index types in Milvus.